Datos bidimensionales

Analizaremos aquí las representaciones gráficas de pares de datos. En concreto, la forma de representar un Diagrama de Dispersión, también denominado Nube de puntos con la función plot analizando alguna de sus muchas posibilidades, así como la manera de representar sobre ella la recta de regresión o mínimos cuadrados.

Una característica relacionada con la bondad de ajuste de esta recta a los datos que forman la nube de puntos es el Coeficiente de correlación lineal de Pearson. Éste se calcula con la función cor.

Ejemplo 2.4

Tras preguntar a 20 personas con aficiones atléticas la marca que poseían en 100 metros lisos y las horas semanales que, por término medio, dedicaban a entrenar se obtuvieron los siguientes datos

Horas	21	32	15	40	27	18	26	50	33	51
Marca	13.2	12.6	13	12.2	15	14.8	14.8	12.2	13.6	12.6

Horas	36	16	19	22	16	39	56	29	45	25
Marca	13.1	14.9	13.9	13.2	15.1	14.1	13	13.5	12.7	14.2

Si queremos representar estos pares de datos (x,y) debemos utilizar la función plot(x,y):

x <- c(21, 32, 15, 40, 27, 18, 26, 50, 33, 51, 36, 16,
       19, 22, 16, 39, 56, 29, 45, 25)
y <- c(13.2, 12.6, 13, 12.2, 15, 14.8, 14.8, 12.2, 
       13.6, 12.6, 13.1, 14.9, 13.9, 13.2, 15.1, 14.1, 
       13, 13.5, 12.7, 14.2)
plot(x, y)

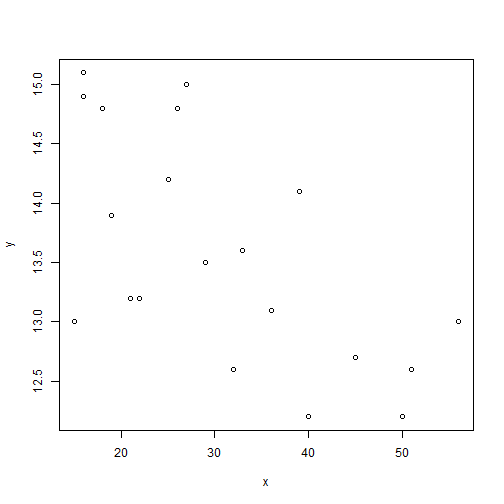
A continuación mostramos los diferentes argumentos de la función:

#Pone titulo y color a los puntos

plot(x, y, main = "nube de puntos", col=3)

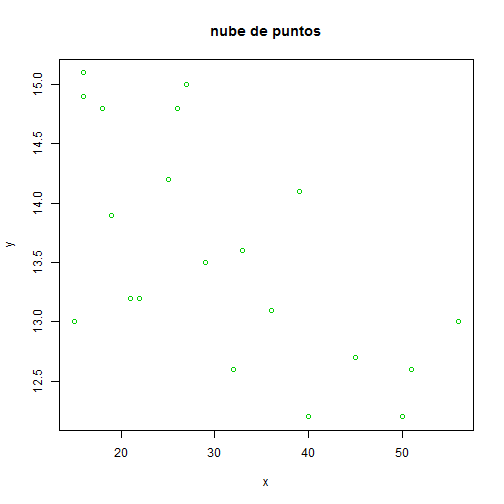
#Limita el recorrido del gráfico

plot(x, y, xlim = range(x), ylim = range(y))

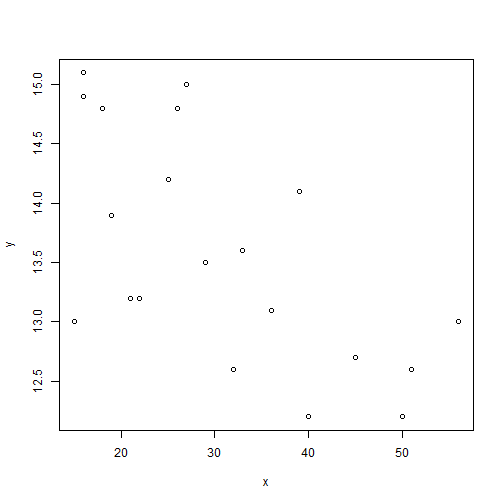
#Pone los puntos como un 2

plot(x, y, pch ="2")

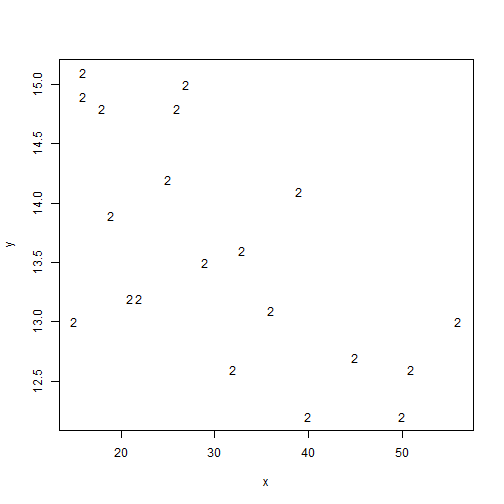
#Pone los puntos como el símbolo x. Hay del 0 al 18

plot(x, y, pch = 4)

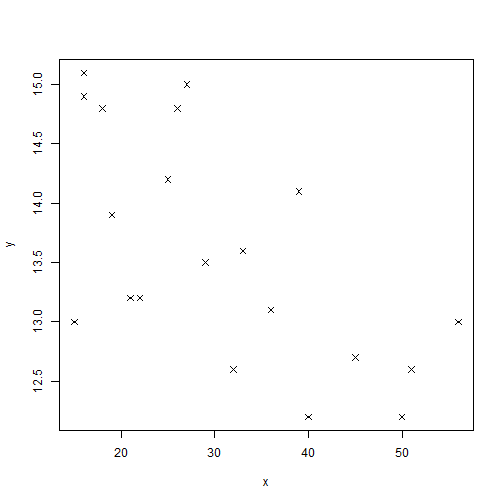
#Pone nombre a los ejes

plot(x, y, xlab = "abcisa", ylab = "ordenada")

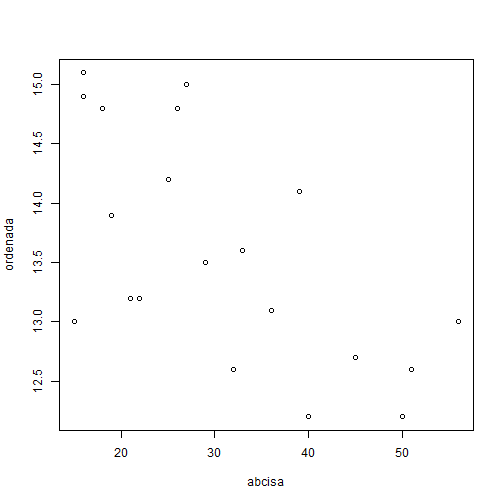
#No pone ningún nombre a los ejes

plot(x, y, xlab = "", ylab = "")

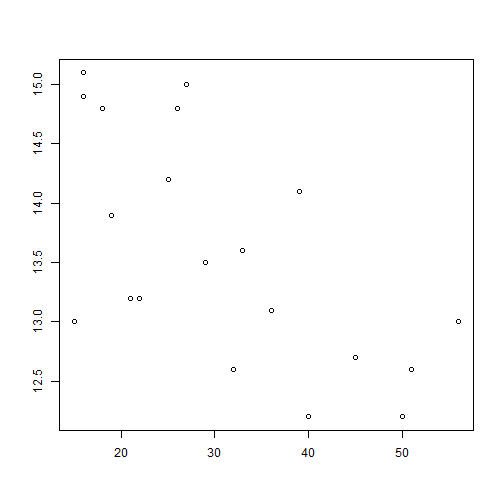
#No pone el marco al gráfico

plot(x, y, axes = F)

Como sabemos, un elemento muy asociado a esta clase de datos es su recta de mínimos cuadrados o de regresión. Podemos obtenerla ejecutando la función lm.

ajus <- lm(y ~ x)
ajus

## 
## Call:
## lm(formula = y ~ x)
## 
## Coefficients:
## (Intercept)            x  
##    15.05908     -0.04786

Obsérverse que hemos obtenido la recta punto-pendiente con ordenada en el origen 15,06 y pendiente -0.048.

Podemos ahora añadirla sin más a la nube de puntos:

plot(x, y, main = "Nube de puntos y Recta")
abline(ajus, col=4)
legend(35, 14.6, c("Línea de regresión"), lty = c(1), col=4)

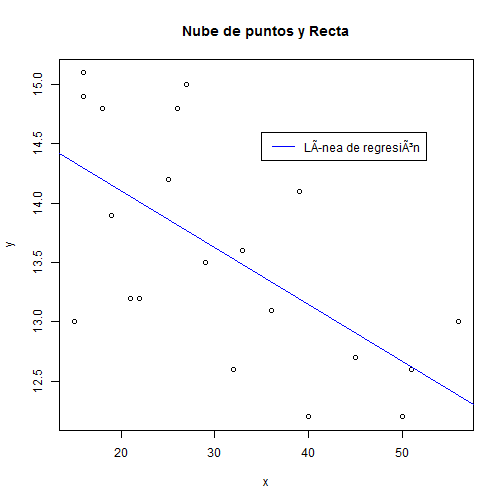
Como dijimos más arriba si queremos calcular el valor del coeficiente de correlación lineal de Pearson, relacionado con la precisión del ajuste de mínimos cuadrados efectuado, ejecutamos:

cor(x, y)

## [1] -0.6304069